Funkcio (matematiko)
Matematikaj funkcioj |
|---|
Fonto-aro, Celo-aro, Bildo, Prabildo |
Fundamentaj funkcioj |
algebraj funkcioj: konstanta • lineara • kvadrata • polinoma • racionala • Transformo de Möbius ceteraj funkcioj: trigonometriaj • inversa trigonometria • hiperbola • eksponenta • logaritma • potenca |
Specialaj funkcioj |
erara • β • Γ • ζ • η • W de Lambert • de Bessel |
Nombroteoriaj funkcioj: |
τ • σ • de Möbius • φ • π • λ |
| Ecoj: |
pareco kaj malpareco • monotoneco • bariteco • periodeco • disĵeteco • surĵeteco • dissurĵeteco kontinueco • derivaĵeco • integralebleco |
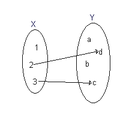
Estu aroj X kaj Y. Oni diras, ke funkcio f ĵetas X al Y, simbole
- f:X→Y{displaystyle f:Xto Y}
se f estas tia rilato super X×Y{displaystyle Xtimes Y}, ke por ĉiu x∈X{displaystyle xin X} en f ekzistas nur unu dupo (x,y)∈f{displaystyle (x,y)in f}; en tia okazo oni skribas y=f(x){displaystyle y=f(x)}.
La aron X oni nomas la fonta aro, simbole iam D(f); la aron Y, la cela aro, simbole iam E(f).
Kutime oni uzas la terminon funkcio se la aroj X kaj Y estas nombraj; en okazoj pli ĝeneralaj oni ankaŭ povas uzi la terminojn ĵeto aŭ bildigo.
La skribmanieron y = f(x) oni nomas funkcia nnotacio, kie x estas sendependa variablo, kaj y - dependa variablo.
Sendependa variablo (la argumento) - la variablo, por ĉiu el kies valoroj estas donita responda valoro de funkcio.
Dependa variablo (la rezulto) - la variablo donita per la valoroj de de funkcio; ekz. en la funkcio sin, x - estas la sendependa variablo (argumento), dum sin x estas dependa variablo.
La rilaton, kiu konsistigas la funkcion, oni povas prezenti kiel regulon, determinantan rezulton por ĉiu argumento. La rimedoj por esprimi la regulon povas esti diversaj:
Tabela - per la vicoj de argumentoj kaj ĝiaj konformaj signifoj;
Grafika - la aro de la punktoj M(x;y) sur la kartezia sistemo, prezentita laŭ formo de la rekto aŭ kurbo;
Analitika - per formulo, ekz. y = 3 x² + 1.
Derivaj difinoj |
- Funkcio estas kreskanta sur iu aro, se por ajnaj elementoj de la aro x₁ < x₂, la malegalaĵo f(x₁) < f(x₂) estas vera. Se por x₁ < x₂, veras la alia malegalaĵo f(x₁) > f(x₂), la funkcio nomiĝas malkreskanta. Ekzemple, funkcio y=x² estas malkreskanta en la intervalo ]-∞;0] kaj estas kreskanta en la intervalo [0;+∞[.
- Funkcio estas para, se la kampo de difino estas simetria rilate al 0 kaj por ajna x ∈ D(f) estas vera egelaĵo : f(-x) =f(x). Kaj ĝi nomiĝas malpara, se veras : f(-x) = -f(x). Ekzemple, y=x² funkcio estas para, kaj y=x aŭ y=x³ estas malparaj.
- Funkcio estas perioda kun periodo p, kiu ne egalas al 0, se por ajna x ∈ D(f) la nombroj x-p kaj x+p ankaŭ apartenas al D(f) kaj veras la egalaĵo: f(x+p) = f(x), ankaŭ f(x) = f(x-p) kaj f(x) = f(x+kp), kie k estas entjero.
- Funkcio estas konveksa, se D(f) estas konveksa aro kaj por ajnaj x kaj y el D(f) kaj t ∈ [0;1] estas vera la neegalaĵo :
f(tx+(1−t)y)⩽tf(x)+(1−t)f(y).{displaystyle f(tx+(1-t)y)leqslant t,f(x)+(1-t),f(y).}
Konveksa funkcio estas kontinua sur D(f) se D(f) estas malferma intervalo, aŭ ĝenerale malferma konveksa subaro de Rn.
inversa funkcio al funkcio f:X→Y{displaystyle fcolon Xto Y}, estas funkcio f−1:Y→X{displaystyle f^{-1}colon Yto X}, de kiu kunaĵo kun funkcio f estas idento-rilato:
(f−1∘f)(x)=x{displaystyle (f^{-1}circ f)(x)=x} por ĉiuj x ∈ X kaj
(f∘f−1)(y)=y{displaystyle (fcirc f^{-1})(y)=y} por ĉiuj y ∈ Y
Vidu ankaŭ |
- Kontinua funkcio
- Lineara funkcio
- Polinoma funkcio
- Eksponenta funkcio
- Trigonometria funkcio
- Speciala funkcio
- Nulo de funkcio
Disĵeta funkcio
Surĵeta funkcio
Dissurĵeta funkcio
Eksteraj ligiloj |
- http://functions.wolfram.com
- http://archives.math.utk.edu/visual.calculus
- http://math.hws.edu/xFunctions
- http://geography.about.com/library/misc/bl2capitals.htm
http://archive.numdam.org/article/CM_1954-1956__12__81_0.pdf La kanonaj formoj de la 2, 3, 4 -dimensiaj paraanalitikaj funkcioj]. Far M. R. Fréchet, en Esperanto, en Revuo Compositio Mathematica, 12 (1954-1956), p. 81-96, formo PDF.