Bxdty

En geometrio, senpintigo aŭ simpla tranĉo estas operacio, plenumebla en ĉiu dimensio, kiu tranĉas verticojn de hiperpluredro, kreante novan faceton anstataŭ ĉiun verticon.

La operacio povas esti farita ĝis diversa grado de profundo. Ju pli profunda estas la tranĉo, des pli mallongaj iĝas la originalaj lateroj kaj des pli grandaj estas la novaj facetoj. La operacio, kiu faras la longon de la originalaj lateroj egala al nulo, nomiĝas rektigo.

Eblas ankaŭ eĉ pli profunda tranĉo. La operacio, per kiu la originalaj edroj iĝas punktoj, nomiĝas durektigo; la operacio, per kiu la originalaj ĉeloj iĝas punktoj, nomiĝas estas trirektigo ktp.

Kiam la termino estas aplikata al regula hiperpluredro aŭ regula kahelaro, oni kutime subkomprenas la uniforman tranĉon, do tranĉon, kies rezulto estas uniforma hiperpluredro aŭ uniforma kahelaro. Se la fonta formo havas simbolon de Schläfli {p₁,p₂,...,p_n-1}, do la uniforma tranĉita formo estas priskribata per etendita simbolo de Schläfli t_0,1{p₁,p₂,...,p_n-1}.

Tranĉo de regulaj pluredroj kaj 2-kahelaroj |

Dum uniforma tranĉo de platonaj solidoj aŭ kahelaro de regulaj plurlateroj la originalaj edroj iĝas regulajn plurlaterojn kun duobla kvanto de lateroj.

Ĉi tiu vico montras la tranĉon de kubo, je kvar ŝtupoj de kontinua senpintiganta procezo inter la fonta kubo kaj rektigita kubo. La meza formo estas la uniforma senpintigita kubo.

Aliaj tranĉoj |

En kvazaŭregulaj pluredroj, tranĉo estas pli kvaliteca termino, kiu subkomprenas ke post la tranĉo iuj malformigoj estas faritaj por adapti senpintigitajn edrojn por ke ili iĝu regulajn.

Ekzemple, la senpintigita kubokedro ne estas reale tranĉo de verticoj de la kubokedro, ĉar post reala tranĉo aperas ortangulaj edroj kiuj ne estas kvadratoj.

Por la katalunaj solidoj, alterna tranĉa operacio estas uzata, kiu senpintigas nur alternajn verticojn. Ĉi tiu operacio povas esti farita nur je pluredro ĉiuj edroj de kiu havas paran kvanton de verticoj, inkluzive zonopluredrojn. (Vidu plu en alternado (geometrio).)

Ekzemploj |

Regulaj pluredroj kaj 2-kahelaroj |

Ĉi tie estas montritaj diversgradaj tranĉoj inter la du regulaj formoj (dualaj unu al la alia), kun la rektigita formo (plena tranĉo) en la centro. Kompareblaj edroj estas kolorigita samkolore. Noto ke en multaj okazoj diversaj formoj koincidas, iam kun turno, movo aŭ reskaligo.

Familio (simbolo de Schläfli)	Originala	Tranĉita	Rektigita	Dutranĉita (senpintigita duala)	Durektigita (duala pluredro)
{3,3}	Kvaredro	Senpintigita kvaredro	Okedro	Senpintigita kvaredro	Kvaredro
{4,3}	Kubo	Senpintigita kubo	Kubokedro	Senpintigita okedro	Okedro
{5,3}	Dekduedro	Senpintigita dekduedro	Dudek-dekduedro	Senpintigita dudekedro	Dudekedro
{6,3}	Seslatera kahelaro	Senpintigita seslatera kahelaro	Tri-seslatera kahelaro	Seslatera kahelaro	Triangula kahelaro
{7,3}	Seplatera kahelaro	Senpintigita seplatera kahelaro	Rektigita seplatera kahelaro	Senpintigita ordo-7 triangula kahelaro	Ordo-7 triangula kahelaro
{8,3}	Oklatera kahelaro	Senpintigita oklatera kahelaro	Rektigita oklatera kahelaro	Senpintigita ordo-8 triangula kahelaro	Ordo-8 triangula kahelaro
{4,4}	Kvadrata kahelaro	Senpintigita kvadrata kahelaro	Kvadrata kahelaro	Senpintigita kvadrata kahelaro	Kvadrata kahelaro
{5,4}	Ordo-4 kvinlatera kahelaro
{5,5}	Ordo-5 kvinlatera kahelaro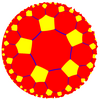

Prismaj pluredroj |

Familio (simbolo de Schläfli)	Originala	Tranĉita	Rektigita	Dutranĉita (senpintigita duala)	Durektigita (duala pluredro)
{2,p}	Seslatera duvertica pluredro (Kiel sfera kahelaro) {2,p}	Seslatera prismo t{2,p}	Seslatera duedro (Kiel sfera kahelaro) {p,2}	Dekdulatera duedro {2p,2}	Seslatera duedro (Kiel sfera kahelaro) {p,2}

Rektigitotranĉitaj (rombotranĉitaj) formoj |

Ĉi tiuj formoj estas rezultoj de senpintigo de rektigitaj regulaj formo. La verticoj estas ordo 4, kaj vera geometria tranĉo devus krei ortangulajn nekvadratajn edrojn. La uniformeco de la rezulto postulas adaptiĝon por krei kvadratajn edrojn. Ankaŭ, senpintigo de rektigo de la fonta formo estas lateroverticotranĉo de la fonta formo.

Originala	Rektigita	Rektigitotranĉita (lateroverticotranĉita)
Kubo	Kubokedro	Senpintigita kubokedro (lateroverticotranĉita kubo) (rombotranĉita kubokedro)
Dekduedro	Dudek-dekduedro	Senpintigita dudek-dekduedro (lateroverticotranĉita dekduedro) (rombotranĉita dudek-dekduedro)
Seslatera kahelaro	Tri-seslatera kahelaro	Granda rombo-tri-seslatera kahelaro (lateroverticotranĉita seslatera kahelaro) (senpintigita tri-seslatera kahelaro)

Regulaj plurĉeloj kaj 3-kahelaroj |

Regula plurĉelo aŭ 3-dimensia kahelaro {p,q,r} post senpintigo iĝas uniforman plurĉelon aŭ 3-kahelaron kun du specoj de ĉeloj:

• t_0,1{p,q} kiuj estas senpintigoj de {p,q} kreitaj el la originalaj ĉeloj;


• {q,r} kreitaj anstataŭ la originalaj verticoj.

Vidi: uniforma plurĉelo kaj konveksa uniforma kahelaro de eŭklida 3-spaco.

Familio (simbolo de Schläfli {p,q,r})	Originala	Tranĉita	Rektigita (durektigita duala)	Dutranĉita (dutranĉita duala)
{3,3,3}	5-ĉelo (mem-duala)	Senpintigita 5-ĉelo	Rektigita 5-ĉelo	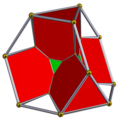Dutranĉita 5-ĉelo
{3,3,4}	16-ĉelo	Senpintigita 16-ĉelo	Rektigita 16-ĉelo (24-ĉelo)	Dutranĉita 16-ĉelo (dutranĉita 4-hiperkubo)
{4,3,3}	4-hiperkubo	Senpintigita 4-hiperkubo	Rektigita 4-hiperkubo
{3,4,3}	24-ĉelo (mem-duala)	Senpintigita 24-ĉelo	Rektigita 24-ĉelo	Dutranĉita 24-ĉelo
{3,3,5}	600-ĉelo	Senpintigita 600-ĉelo	Rektigita 600-ĉelo	Dutranĉita 600-ĉelo (dutranĉita 120-ĉelo)
{5,3,3}	120-ĉelo	Senpintigita 120-ĉelo	Rektigita 120-ĉelo
{4,3,4}	Kuba kahelaro (mem-duala)	Senpintigita kuba kahelaro	Rektigita kuba kahelaro	Dutranĉita kuba kahelaro
{3,5,3}	Ordo-3 dudekedra kahelaro (mem-duala)	Ordo-3 senpintigita dudekedra kahelaro	Ordo-3 rektigita dudekedra kahelaro	Ordo-3 dutranĉita dudekedra kahelaro
{4,3,5}	Ordo-5 kuba kahelaro	Ordo-5 senpintigita kuba kahelaro	Ordo-5 rektigita kuba kahelaro	Ordo-5 dutranĉita kuba kahelaro (Ordo-4 dutranĉita dekduedra kahelaro)
{5,3,4}	Ordo-4 dekduedra kahelaro	Ordo-4 senpintigita dekduedra kahelaro	Ordo-4 rektigita dekduedra kahelaro
{5,3,5}	Ordo-5 dekduedra kahelaro (mem-duala)	Ordo-5 senpintigis dekduedra kahelaro	Ordo-5 rektigita dekduedra kahelaro	Ordo-5 dutranĉita dekduedra kahelaro

Vidu ankaŭ |

• Operacioj je hiperpluredroj kaj kahelaroj:
  
  
  
  • 
    Tranĉo t_{0, 1}{p, ...}
  
  
  • 
    Laterotranĉo t_{0, 2}{p, q, ...}
  
  
  • 
    Lateroverticotranĉo t_{0, 1, 2}{p, q, ...}
  
  
  • 
    Edrotranĉo t_{0, 3}{p, q, r, ...}
  
  
  • 
    Edroverticotranĉo t_{0, 1, 3}{p, q, r, ...}
  
  
  • 
    Edrolaterotranĉo t_{0, 2, 3}{p, q, r, ...}
  
  
  • 
    Edrolateroverticotranĉo t_{0, 1, 2, 3}{p, q, r, ...}
  
  
  • 
    Ĉelotranĉo t_{0, 4}{p, q, r, s, ...}
  
  
  • 
    Entutotranĉo t_{0, 1, ..., n-1}{p₁, p₂, ..., p_n-1}
  
  
  • 
    Rektigo t₁{p, ...}
  
  
  • 
    Dutranĉo t_{1, 2}{p, q, ...}
  
  
  • Alternado
  
  
  • Riproĉigo
  
  
  
  


• 
  Simbolo de Schläfli - etendita simbolo de Schläfli priskribas rezultojn de la operacioj faritaj je regulaj hiperpluredroj kaj regulaj kahelaroj
  

• Uniforma pluredro


• Uniforma plurĉelo

Eksteraj ligiloj |

• Tranĉo en MathWorld


• 
  George Olshevsky, Tranĉo en Glossary for Hyperspace.